A clever statistical technique for low count events

Even the gold standard study design, randomized clinical trials, have issues with confounding and selection bias in low count settings - especially if less is known about the disease in question. In some genetics research a correction calculation is used to counter lag error caused by under counting the true disease prevalence. The method is called mandelian randomization as it conceptually represents a randomized trial where alleles are considered random instrumental variables and the disease symptoms are the outcome. This conceptual model allows the exposure to be a risk factor of the disease, rather than the allele itself.

The premise goes like this..

Natural genetic variation will produce multiple randomized trials of alleles, giving different risk factors (exposures) and producing the disease symptoms (outcomes). In other words each level of exposure-risk is a unique observation, rather than each allele. So the number of observations can be much greater even if few alleles are studied.

Why a public health student like me cares..

Other than being an interesting method, population health studies could use a similar model. By making patient behaviors instrumental variables, risk factor of disease the exposures, and diseases symptoms the outcomes; low prevalence diseases could be studied with potentially better results. This segments one patient observation into many behavioral observations. The trick is identifying behaviors which are mostly random in a population, or at least have well known confounders to correct for not being totally random. This catch is a major hurdle, but a solvable one.

The conceptual model..

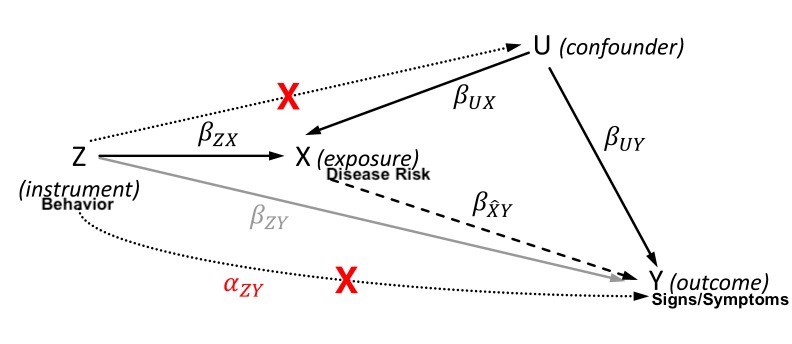
In the mendelian randomization example, researchers use 2 stage least squares regression to find confounding measurement errors.

Link to a figure from the cited paper, above the description of 2SLS and alternative ratio estimator calculations

The conceptual model assumes that the causal relationship from instrument to outcome is a product of [instrument –> exposure] and [exposure –> outcome]. So the effect of the instrumental variable divided by the effect of the instrument on the outcome is the effect of the estimate on the outcome.

B_ZY = B_ZX * B_XY

B_ZX: B_XY = B_ZY / B_ZX

For an alternative ratio estimator triangulation method, researchers can calculate the control function estimator by regressing exposure X on instruments Z, then use this result as the covariate in the logit: Y ~ X + covar. This method is equivalent to 2SLS if a linear regression is used instead of logistic regression.